找对象作为人生头等大事之一，自然是被运筹学者们好好研究过一番了。今天我们就从数学模型的角度，探究一下男生和女生是否可以通过一些策略，来让自己找到更心仪的对象。这里先剧透结论：在以男追女为主导的世界中，男性没有任何策略可以改变自己的形势，而女性则有机会通过伪造自己的择偶偏好来获得更好的归宿。

我们先提出一个最简单的设定：假如这个世界上只有想找女生的直男和想找男生的直女，并且数量相等。（这里忽略掉 LGBTQ 群体和不找对象的群体，我相信未来一定会有考虑少数群体的模型出现的！）接下来，我们假设这个世界都是男生主动追女生，没有女追男的情况发生，但是所有的男性在自己的心里都把所有的女性排了个序，所有的女性也在心里把所有的男生排了个序。把“所有异性排序”其实并不需要一开始就认识所有人，只要每认识一个新的异性时，能够把他和已经认识的异性作比较即可。在最基本的模型中，我们先假设女生即便不是很喜欢追她的男生 A，也不会拒绝，而是“先处着”：如果之后遇到了更心仪的追求者 B，她会拒绝之前的 A，从了新的追求者 B。而 A 会把这个女生从他的心中划掉，寻找其他还在他心中的女生（后面我们会考虑女生可以直接拒绝的情况）。在经过反反复复配对之后，当所有人的恋爱关系稳定之后，大家才会结婚。我们的目标是研究人们是否可以通过特定的策略，使自己最终的结婚对象更好一点。

下面举一个三男三女的小例子：男生用 ABC 来表示，女生用 123 来表示。对于 A 来说，他最喜欢 1 号女嘉宾，3 号次之，2 号最将就。对于 1 号女嘉宾来说，B 是她的最爱，A 次之，C 只能算备胎。

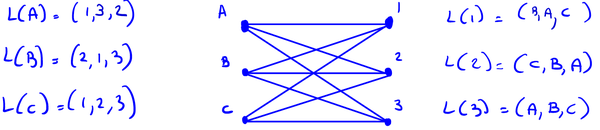
那么什么样的配对算是稳定呢？我们认为一旦符合下列条件，这种配对就是稳定的：对于任何男女 A 和 2，他们之间的关系满足下列三种条件之一：

1. 他俩是一对儿。

2. 在 A 心里他的对象比 2 号女嘉宾要好。

3. 在 2 号女嘉宾心里，她的对象比 A 要好。

其实这个条件翻译成人话就是：对于任何人来说，你当前的对象可能不是最满意的，但比她 / 他更好的都看不上你。同时，你也有可能是别人的菜，但喜欢你的人都还不如你现在的对象。假如这个世界上存在一个你更喜欢的人刚好更喜欢你，那你俩就会离开当前的对象在一起，这样的配对就是不稳定的。稳定的配对方式可能不止一个，在上面的例子中，一个稳定的配对方式是 A 配 3，B 配 1，C 配 2.在这样的配对方式下，谁都没有分手找新对象的动力。

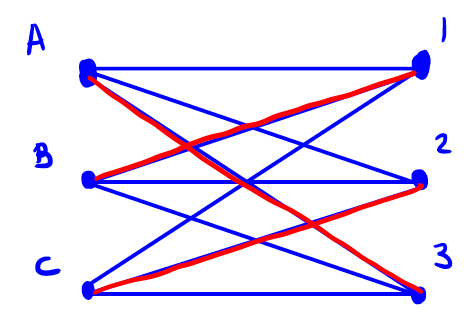
我们首先讲如何找到稳定的配对。实际上，Gale 和 Shapley 提出了一个算法，这种算法可以很快的得到稳定的配对，并且可以较好的类比现实生活。Gale-Shapley 算法是这样的：

假设大家开始都没有对象。在单身的男生里随机选一个 X，该男生追他心中最喜欢的女生。如果该女生没有对象，就暂时接受这个男生；如果该女生已经有对象并且比 X 要好，就不会发生改变，同时 X 被拒绝后在心中删掉该女生；如果觉得目前的对象没有 X 好，就跟 X 配对，而前任则恢复没有对象的状态，并且在心中删掉这个女生。重复这个过程直到所有的男生（以及女生）都有对象。

对应到我们的小例子中：假如 A 最早熟，先追了女神 1 号，1 号觉得还 OK 就先处着。接着在单身的 B 和 C 里，让 B 追女生，他选择他的女神 2 号，2 号觉得还 OK 就先处着。最后单身的 C 选择女神 1 号，可是 1 号心里 C 还不如 A，拒绝了 C。于是单身的 C 心里只剩下了 2 和 3，他选择追 2 号女生。2 号觉得 C 比 B 要好，于是选择跟 C 在一起，B 恢复单身并在心中拉黑 2 号。单身的 B 心中还剩下 1 号和 3 号，所以他选择追 1 号。1 号觉得 B 比 A 要好，所以选择跟 B 在一起，A 恢复单身并在心中拉黑了 1 号。最后，单身的 A 心里还剩下 3 号和 2 号，他去追 3 号，一直无人问津的 3 号和最先早熟的 A 在一起，配对完成。最终的结果就是我们之前提到的稳定配对 A-3，B-1，C-2.

Gale-Shapley 算法虽然听起来有一种“贵圈真乱”的感觉，但是当整个系统中的男女数量很大时，它还是很好的模拟了男追女的过程。这个算法除了保证得到稳定的配对之外，还有下面的特点：

1. 男性最优(men-optimal)：不存在另一种稳定配对，在该配对中某个男生可以找到更好的女生。
2. 女性最劣(women-pessimal)：不存在另一种稳定配对，在该配对中某个女生会找到更差的男生。
3. 弱帕累托最优(weakly Pareto-optimal)：不存在任何配对（无论稳定或不稳定），所有男生都可以找到更心仪的对象。

看到这里女生们可能就不爽了，果然男性主导的婚姻市场就是对女生不利的。其实也没有那么差啦，如果看我们上面的小例子，所有的男生都只找到了第二喜欢的女生，而所有的女生都找到了自己最喜欢的男生。

接下来就到了我们探究的重头戏：有没有可能，人们可以通过伪造自己心中的择偶次序来获得更好的结果呢？比如一个男生，他可能跟自己最不喜欢的姑娘在一起了，他会想，如果当初假装不喜欢女神（声称她在心里最末尾的位置），或者直接放弃追女神（直接把她从心里删除，即网络图中两人没有连线），改追还 OK 的女生，我是不是能跟更心仪的女生在一起呢？

非常残酷的是，在 Alvin Roth 1982 年的论文中已经证明，假如其他人不撒谎的话，无论是假装不喜欢还是直接放弃，该男生最好只能追到不撒谎状态下的那个女生。当然了，全局的形势可能变好。例如在我们的例子中，男生 A 如果放弃了女神 1 号，最终的配对结果会是 A-3,B-2,C-1.A 同学放弃了自己的女神，让 B 和 C 追到了自己的女神，站在男性整体的角度确实变好了嗯……但是谁愿意做 A 呢？更不要说 1 号和 2 号就无法跟自己最心仪的男生在一起了，成全了自己的情敌还委屈了自己的女神，这波操作实在是 666。

那么对于女生来说呢？有没有可能通过假装不喜欢男神（声称他在心里末尾的位置），或者假如她单身时就可以直接拒绝任何男生而不是先处着（直接把这个男生从心里删除，即网络图中两人没有连线），最终使自己找到更好对象呢？

答案是可以的！

如果这个世界是女追男的话，那么我们可以得到一个女性最优的配对(women-optimal)。这个配对结果对于女生来说不会差于男追女的结果。假如女生知道在女追男的世界中自己的归宿是 X，并且比男追女的世界中的对象 Y 要好，她可以怎么做呢？Gusfield and Irving (1989)证明了，如果她没有拒绝的权利，那她可以通过打乱自己心中的次序，让 X 排在首位，来锁定 X。而 Gale and Sotomayor (1985)这篇论文里，如果女生有拒绝任何人的权利，她可以声称比 X 更差的男生全不能接受来锁定 X。也就是说，假如一个女生存在两个以上稳定配对的男生，不管有没有拒绝的权利，女生总有机会通过伪造择偶次序来获得更好的结果。这个看上去由男性主导的恋爱市场，其结果完全可以被女性决定。

所以我们的结论是：

对于男生来说，你唯一能做的就是对自己喜欢的女生展现自己的全貌，然后等待一个结果，任何策略都是徒劳的。

对于女生来说，如果你能准确地估计在女追男的世界中自己最终的对象是什么样的人，那么你可以提前调整自己的择偶标准或排序，从而避免更差的归宿。当然了，错误的判断会带来更差或者孤独一生的结果。

估计自己在女追男的情况下对象是怎样的，听起来还挺难的是不是？实际上，上面结论的前提是一个女生存在两个以上稳定配对的男生（或者说，当我们用一个男生代表一类男生的时候，两类特点不同的人）。有很多文章都提到了这样的女性其实很少。例如，在 Teo et al (2001)中，作者模拟了这个过程，发现假如有 1000 种男女的话，能够通过说谎获益的女性只有 5.06%。所以，对于女性来说，假如不能准确估计主动出击的结果的话，遵从自己的内心很大可能不会变得更差。

不过嘛，人们总会相信自己就是能估计未来的归宿，并且相信自己就是那一小部分可以改变命运的人（滑稽）。那么 OK，感情问题嘛折腾一下也没有什么，不后悔就好了。但我想说的是，稳定婚姻模型被广泛应用在求职、升学报志愿等问题上，求职者和学生作为被动的一方，也就是男追女婚姻模型中的女性，还是诚实面对自己内心的排序风险比较小。

这个研究给我们的启示：

感情问题里主动的一方不一定能获得更好的结果，在绝大部分情况下谁主动对结果影响不大，都是缘分；

如果一个女生声称她要找“经济适用男”，那么她的动机是合乎理性的；

如果一个学生号称自己非清华不上，那么他可能就要失学了……

参考文献:

Gale, D., M. Sotomayor (1985a). Some Remarks on the Stable Matching Problem.

Discrete Applied Mathematics 11 223-232.

Gale, D., M. Sotomayor (1985b). Ms Machiavelli and the Stable Matching Problem.

American Mathematical Monthly 92 261-268.

Gusfield, D., R. W. Irving (1989). The Stable Marriage Problem: Structure and

Algorithms, MIT Press, Massachusetts.

Teo, C. P., Sethuraman, J., & Tan, W. P. (2001). Gale-shapley stable marriage problem revisited: Strategic issues and applications. Management Science, 47(9), 1252-1267