先讲一个真实的例子。

1986 年，为了对比肾结石治疗中两种手术的优劣，有人统计了接受这两种手术的病人数量和成功率。在统计中，作者按照严重程度把病人分为大块结石和小块结石两组，然后分别统计了两组病人中手术 A 和手术 B 的成功率。得到的结果可以清晰地展示在下面的这个表格中：

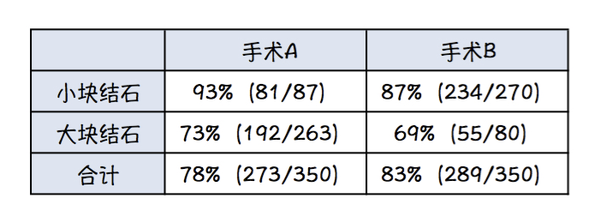
让我们来一行行地看一下这个表格。

先看第一行：对于小块结石的病人，手术 A 的成功率为 93%，手术 B 的成功率只有 87%。很明显，手术 A 胜出。（表格中百分比后面的两个数字分别是成功案例数 / 总案例数）。

我们再看第二行：对于大块结石的病人，手术 A 的成功率为 73%，手术 B 的成功率只有 69%。手术 A 再次胜出。

数字是不会说谎的。看到这里，我们似乎已经可以得出结论了：无论对于小块结石还是大块结石的病人来说，手术 A 都有着较高的成功率。这个结论背后有坚实的数据作为支撑，证据确凿，铁证如山。

如果你得出了这样一个结论，请继续往下看第三行，你的内心可能会在一瞬间崩溃。

第三行中不再把病人分为大小结石两组，而是显示了每种手术在所有病人中的成功率。根据第三行的数据，手术 A 在所有病人中的成功率为 78%，手术 B 在所有病人中的成功率为 83%。这样看起来，好像手术 B 的成功率又比较高！

WTF！为什么分开比较时手术 A 在每组病人中都有较高的成功率，但进行合计后手术 B 反而有较高的成功率？这听起来是一件不可能的事情，一定是表格中某个数字算错了。但你可以把表格中的数字随便检查多少遍，你会发现每一个数字都是正确的。

有兴趣的话，你可以先自己琢磨一下这究竟是怎么回事，然后再接着往下读。

在统计学的世界中，数字不但会说谎，而且它有时还是一个谎话连篇的碧池。如果仔细观察一下上面表格中的数字，你会发现前两行四个格子里的手术数量并不是均匀分布的。右上角和左下角的格子里集中了更多的手术，这是因为医生在面对小块结石时，更倾向于选择较小的手术 B，而在面对大块结石时，则更倾向于选择大手术 A。换句话说，医生在为病人选择手术种类时，已经无意识中影响了最后的统计结果。

由于在总样本中占据了较大的数量，右上和左下的两个格子中的成功率对比直接决定了合计行中两种手术的成功率对比。所以这个结果这与我们的直觉正好相反：直觉告诉我们如果手术 A 在两组病人中都更好，那么在所有病人中也应该更好。

评论中有人说答主故意编造了一组数据来误导大家，其实不是的。这是一个人们在统计手术成功率时发生的真实案例，维基上有这篇医学论文的题目：Comparison of treatment of renal calculi by open surgery, percutaneous nephrolithotomy, and extraco。这种违背人类直觉的现象在统计学中还有一个专门的名称，叫做 Simpson's Paradox。

翻翻这个问题下的答案，你会发现大部分违反人类直觉的问题都和概率统计有关。这是因为我们的大脑和几万年前原始人的大脑没有太大区别。在几百万年的进化中，我们的直觉可以很好地引导我们理解大小、高低、速度这些直观的概念，但对于概率统计中极度抽象的概念，我们的直觉就不管用了。

在医学统计中犯下这种错误，会让你得出一个错误的结论。而在法庭中犯下这样的错误，则可能会把一个无辜的人送进监狱。

在 1996 年和 1998 年，英国女性 Sally Clark 的两个年幼的儿子先后突然死亡。1999 年，警方逮捕了 Clark，罪名是谋杀自己的两个儿子。在法庭上，一名不懂概率学的儿科医生作证说“同一个家庭中，有两名婴儿自发突然死亡的概率是七千三百万分之一”。根据统计数字，平均大约每 8500 个家庭中会发生一起婴儿自发突然死亡事件，于是这个儿科医生就想当然地将两个 1/8500 相乘，作为一个家庭中先后发生两次自然死亡事件的概率。

同样不懂概率学的法官又凭借直觉把这个概率等同于 Clark 无罪的概率，最后判决 Clark 有罪。Sally Clark 在蹲了三年多的冤狱后，这个案子才被平反，她本人在 2003 年出狱。在失去两个儿子和蹲冤狱的双重打击下，这名母亲的精神已经变得非常地不稳定。2007 年，43 岁的 Sally Clark 死于酒精中毒。

在这里，儿科医生的错误计算不是我们讨论的重点（他没有考虑家庭环境、遗传疾病等因素的影响）。我们重点来关注一下法官在这个案子中犯下的错误：一件事发生的概率是否可以直接等同于一个人有罪 / 无罪的概率？

假设我们在一起谋杀犯罪现场找到了一枚凶手留下的指纹，警察将这个指纹和 20000 个人的指纹进行对比后，找到了一个与现场指纹吻合的嫌犯。现在，这名嫌犯被带上法庭，并被指控为杀人凶手。法庭上的专家告诉你，现代的指纹对比技术的正确率为 99.99%。换句话说，这种比对技术把两个人的指纹误认为同一个的几率只有万分之一。（评论中有人说得很对，出错分为“把同一个人的指误认为两个人的”和“把两个人的指纹误认为同一个人的”，为表述方便，我这里的万分之一出错率指的是后一种。）

如果你现在是法官的话，你会怎么去判断这件事情？这是不是意味着这名嫌犯无罪的概率只有万分之一？

我们的直觉让我们很容易得出这样的结论，不是吗？

但如果你这样想的话，你就犯了和 Sally Clark 案中法官一样的错误。

如果警方用来进行对比的 20000 人全部都是无辜群众，那么用凶手的指纹和他们进行逐一对比后，至少产生一例吻合的几率是多少？

答案是 86%。

（评论中有人问这个 86%怎么算出来的，在这里简单说明一下。要计算在 20000 次对比中至少错一次的概率，我们只要计算对比测试连续对 20000 次的概率，然后剩下的就是至少错一次的概率。连续对两万次的概率是 0.9999 的两万次方=0.14，剩下的 0.86 就是至少出一次错的概率。）

也就是说，用这种准确率为 99.99%的方法在两万个无辜的人中去找凶手，你仍然有 86%的概率能至少找到一个倒霉蛋和凶手的指纹对得上。尽管这个人完全是无辜的。

我们的直觉总是让我们忽略这样一个事实：如果重复足够多次数的话，概率再小的事情也会发生。因此，在法庭上绝不能把一件事情发生的概率简单地等同于当事人有罪 / 无罪的概率。

最后我们来讲一下那个经典的三门问题。其他的回答里已经有人讲过这个问题了，但我觉得讲得都不是特别清楚，所以在这里再讲一次。

这个三门问题（Monty Hall problem）最早来源于一个美国的电视节目。在节目中，参赛者会面对三扇门，其中一扇门后是一辆汽车作为奖品，另外两扇门后各有一只山羊。

主持人首先会让参赛者选择一扇门，选定之后，主持人会在剩下的两扇门里打开一扇后面是羊的门（主持人知道车子在哪扇门后），以增加现场气氛。接下来，主持人会问参赛者，你现在还有一次机会换一扇门，要换吗？

很多人（包括答主）在第一次听到这个问题时，都会认为换不换是一样的。因为在主持人打开一扇门之后，还剩下两扇门可供选择，其中一扇后面是奖品，一扇后面是羊。这时参赛者面对的问题变成了两扇门中任选一扇，既然参赛者不知道哪扇门后面是奖品，那么无论选择哪一扇门的中奖率都是 50%。

但是，数学计算表明，这时不换门的中奖率是 1/3，而换门后的中奖率是 2/3。参赛者应该选择换门。

这是一个非常违背人类直觉的结论。对于这个结果，别说是普通人，就是很多数学家一开始都不相信，很多学者对这个问题还进行过激烈的争论。

面对着剩下的两扇一模一样的门，参赛者可以自由地在两扇门之间做出选择，这让人很难理解为什么其中一扇门的概率是 1/3，而另一扇是 2/3。

我现在还记得当年的概率课老师曾经说过：“在酒吧里引发一场斗殴的最好方法就是把这个题讲一遍。”

另外一个答案中贴出了数学计算过程，但我想应该没人有兴趣去看这些公式，所以我在这里试着用简单的语言来推导一下这个结果（这也是我怎么想明白这个问题的）。

假设你是参赛者，在游戏的最开始主持人要求你在三扇门里任选一扇。想象在你选择的一刹那，你的世界分裂成了三个平行世界，每个世界中的你都选择了一扇不同的门。很显然，三个世界里有一个世界中你选对了，另外两个世界中你选错了。记住，每一个世界代表 1/3 的概率。

接下来，在每一个世界中，主持人在剩下的两扇门里打开了一扇有山羊的，然后问你要不要换门。

选择不换门：三个世界中，一个你中奖，两个你没中奖。所以三个世界加起来你的中奖率是 1/3。

选择换门：在原来你中奖的那个世界中，你放弃了正确的门，换成了一个错误的门。但是！在另外两个世界中，你从错误的门换到了正确的门，因为主持人已经帮你排除掉了一个错误的门。三个世界中，一个你没中奖，两个你中奖。所以三个世界加起来你的中奖率是 2/3。

这样讲是不是能让你更好地理解这个问题？

人类的直觉在这个问题中之所以会出错，同样是因为人脑十分不擅长处理与概率有关的数字。问题究竟出在哪里呢？在你做出第一次选择的时候，汽车在你选中的门背后的几率是 1/3，在另外两扇门背后的几率也分别是 1/3。当主持人打开一扇门后，相当于帮你排除掉了一扇门。那么，原来属于这扇门的 1/3 的概率跑到哪里去了呢？这多出来的 1/3 的概率“叠加”在了另外一扇你没有选择的门上，把它的概率增加到了 2/3。这就是为什么换门会有更高的中奖率。

我们的无法看到、也无法感知到这两个 1/3 叠加的过程，所以在这里我们的直觉又不管用了。直觉只会告诉我们，你面前有两扇门，其中一扇里面有奖品，所以每扇门的中奖率是 50%！

PS：

对于我来说，我更喜欢用平行世界这种方式来想明白这个问题，因为说白了平行世界也就是对概率树种不同情况的一个比喻罢了。但我在评论中看到好几个很好的思路，对于有些人来说，可能这些思路理解起来更容易。我在这里汇总一下：

思路一：把 3 扇门扩大到 100 扇。你选中一扇门之后，主持人帮你排除掉 98 扇错误的，这时候换还是不换？凭直觉也能感到应该换了吧。

思路二：如果选择换的话，本质上等于你一开始就同时选择了这两扇门（主持人帮你去掉了一个错误的，等于多送了你一条命）。

---

看到评论里争论得这么激烈，我的概率课老师一定会感到很欣慰。

评论里留言的大部分都是明白选择换门胜率更大的，我想这是因为会做这个题目的人有更多的动力来写评论。如果在现实生活中找一屋子人来问的话，选择换和不换的应该是一半一半，甚至选择不换的更多。